Are Negative Square Roots Rational

Let's investigate what happens when negative values appear under the radical symbol (as the radicand) for cube roots and square roots.

In some situations, negative numbers under a radical symbol are OK. For example, is not a problem since (-2) • (-2) • (-2) = -8, making the answer -2. In cube root bug, it is possible to multiply a negative value times itself three times and get a negative answer.

Difficulties, notwithstanding, develop when we look at a problem such as . This square root problem is request for a number multiplied times itself that will give a production (answer) of -16. There simply is no way to multiply a number times itself and get a negative result. Consider: (four) • (4) = 16 and (-four) • (-iv) = sixteen.

CUBE ROOTS:	BUT	Foursquare ROOTS:
Yes, (-two) x (-2) x (-2) = -eight. No problem.		Nope! (4) x (4) ≠ -sixteen. Nope! (-4) x (-4) ≠ -16.

Square roots are the culprits! The difficulties arise when you come across a negative value under a foursquare root. It is not possible to foursquare a value (multiply it times itself) and arrive at a negative value. So, what do we do?

The square root of a negative number does not exist among the set up of Real Numbers.

When problems with negatives under a square root kickoff appeared, mathematicians idea that a solution did not exist. They saw equations such as x ² + 1 = 0 , and wondered what the solution really meant.

In an effort to address this trouble, mathematicians "created" a new number,

i , which was referred to as an "imaginary number" , since it was not in the set of "Real Numbers". This new number was viewed with much skepticism. The imaginary number offset appeared in print in the year 1545.

The imaginary number "i" is the foursquare root of negative one.

An imaginary number possesses the unique property that when squared, the consequence is negative.

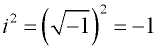
irad1

Consider:
The process of simplifying a radical containing a negative factor is the same equally normal radical simplification. The simply difference is that the will be replaced with an " i ".

Every bit research with imaginary numbers continued, information technology was discovered that they actually filled a gap in mathematics and served a useful purpose. Imaginary numbers are essential to the report of sciences such equally electricity, quantum mechanics, vibration analysis, and cartography.

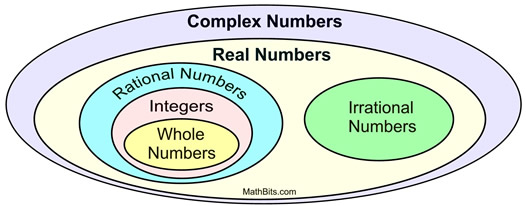
When the imaginary i was combined with the set up of Existent Numbers, the all encompassing set of Circuitous Numbers was formed.

complex

Production Rule

where a ≥ 0, b≥ 0

"The square root of a production is equal to the product of the square roots of each factor."

This theorem allows the states to use our method of simplifying radicals.

Imaginary (Unit) Number

Production Rule
(extended) where a ≥ 0, b≥ 0
OR a ≥ 0, b < 0
but
Non a < 0, b < 0

FYI: The powers of i ever bicycle through only 4 dissimilar values:
i ¹ = i
i ² = -ane
i ³ = -i
i ⁴ = one
i ⁵ = i and the cycle starts over again.

When doing arithmetic on i , treat it as yous would an "x".
3 i + 4 i = 7 i
2 i • 4 i = 8 i ² = -8
Annotation: i ² was replaced with -i.

Do Not misfile "irrational" numbers
with
"imaginary" numbers.
They are NOT the aforementioned.

Complex Numbers
a ± bi
where a and b are real numbers, and i is the imaginary unit.

Complex numbers are written in the standard form a + bi.

In Algebra 1, you will see that the "imaginary" number will be useful when solving quadratic equations. The quadratic formula may requite complex solutions, written as a ± bi, where a and b are real numbers.
Y'all will see more than near imaginary numbers in the Quadratic department.